El movimiento parabólico.

👯💜Definición: 

Se denomina movimiento parabólico, al movimiento realizado por cualquier objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme. El movimiento parabólico es un ejemplo de un movimiento realizado por un objeto en dos dimensiones o sobre un plano. Puede considerarse como la combinación de dos movimientos que son un movimiento horizontal uniforme y un movimiento vertical acelerado.

Fórmulas 😁😀:

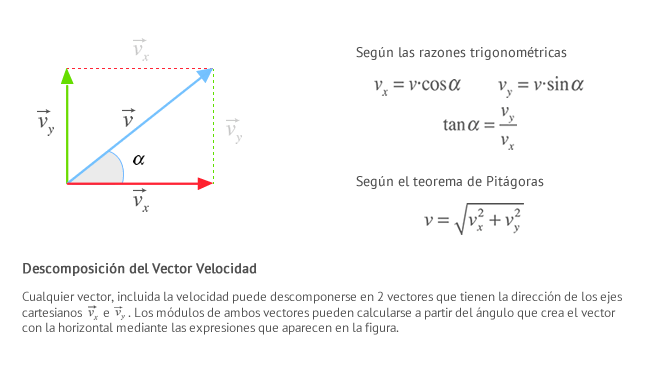
Hay dos ecuaciones que rigen el movimiento parabólico:

donde:

${\displaystyle v_{0}\,}$ es el módulo de la velocidad inicial.

${\displaystyle \phi \,}$ es el ángulo de la velocidad inicial sobre la horizontal.

${\displaystyle g\,}$ es la aceleración de la gravedad.

${\displaystyle \mathbf {i} ,\mathbf {j} }$ son dos versores (vectores unitarios) en el plano.

Leyes 💙👻:

1. Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y la diferencia de alturas (entre salida y llegada) se conocerá toda la trayectoria.
2. Los ángulos de salida y llegada son iguales (siempre que la altura de salida y de llegada sean iguales)
3. La mayor distancia cubierta o alcance se logra con ángulos de salida de 45º.
4. Para lograr la mayor distancia fijado el ángulo el factor más importante es la velocidad.
5. Se puede analizar el movimiento en vertical independientemente del horizontal.

Ejercicios 🙌🙋:

Minuto 90 de juego... Lopera se acerca al balón para lanzar un libre directo a 40 metros exactos de la portería, da dos pasos hacia atrássss y lanzaaaa. El balón describe una trayectoria parabólica y sale con una elevación de 20º... y ¡¡¡¡¡GOOOOLLL!!!! ¡¡¡¡GOOOOOOOLLL!!!! ¡¡¡¡El balón entra por la escuadra a 1.70 metros de altura!!!. Tras oir esta emisión en la radio, ¿sabrías responder a las siguientes preguntas?

a) Desde que Lopera chuta y marca el gol, ¿cuánto tiempo ha transcurrido y a qué velocidad salió el balón desde las botas de Lopera?
b) ¿Qué altura máxima alcanzó el balón?
c) ¿Con qué velocidad llegó el balón a la portería?

Cuestión a):

x=v0⋅cos(α)⋅ty=v0⋅sin(α)⋅t−12⋅g⋅t2}⇒40=v0⋅cos(20)⋅t1.7=v0⋅sin(20)⋅t−12⋅9.8⋅t2}⇒40=v0⋅0.94⋅t1.7=v0⋅0.34⋅t−4.9⋅t2}⇒t=1.61 sv0=26.36 ms/}

Cuestión b)

Cuando la componente y de la velocidad (vy) sea 0 entonces quiere decir que estaremos en el punto más alto de la parábola. Recuerda que comienza a ascender y su velocidad en el eje y va disminuyendo hasta que se anula y comienza a ser negativa para descender.

vy=v0y−g⋅t⇒vy=v0⋅sin(α)−g⋅t ⇒0=26.36 ms/⋅sin(20º)−9.8 ms2/⋅t ⇒t=9.05 ms/9.8 ms2/⇒t=0.92 s

Ahora ya estamos en condiciones, aplicando la ecuación de posición en el eje y, y sustituyendo por el instante que hemos obtenido, de determinar la altura máxima alcanzada:

y=H+v0y⋅t−12g⋅t2⇒y=0+26.36⋅sin(20)⋅(0.92)−12⋅9.8⋅(0.92)2⇒⇒y=4.14 m

Cuestión c)

Sabiendo que el balón llegó a la portería en 1.61 s, su velocidad se obtiene:

vx=26.36⋅cos(20)=24.77 ms/vy=26.36⋅sin(20)−9.8⋅1.61=−6.76 ms/v=vx2+vy2−−−−−−−−√=(24.77)2+(−6.76)2−−−−−−−−−−−−−−−−√=25.67 ms/

El instante en el que el balón llega a la portería x=40 m e y=1.7 m. Sustituyendo en las ecuaciones de la posición del movimiento parabólico:

x=v0⋅cos(α)⋅ty=v0⋅sin(α)⋅t−12⋅g⋅t2}⇒40=v0⋅cos(20)⋅t1.7=v0⋅sin(20)⋅t−12⋅9.8⋅t2}⇒40=v0⋅0.94⋅t1.7=v0⋅0.34⋅t−4.9⋅t2}⇒t=1.61 sv0=26.36 ms/}

Cuestión b)

Cuando la componente y de la velocidad (vy) sea 0 entonces quiere decir que estaremos en el punto más alto de la parábola. Recuerda que comienza a ascender y su velocidad en el eje y va disminuyendo hasta que se anula y comienza a ser negativa para descender.

vy=v0y−g⋅t⇒vy=v0⋅sin(α)−g⋅t ⇒0=26.36 ms/⋅sin(20º)−9.8 ms2/⋅t ⇒t=9.05 ms/9.8 ms2/⇒t=0.92 s

Ahora ya estamos en condiciones, aplicando la ecuación de posición en el eje y, y sustituyendo por el instante que hemos obtenido, de determinar la altura máxima alcanzada:

y=H+v0y⋅t−12g⋅t2⇒y=0+26.36⋅sin(20)⋅(0.92)−12⋅9.8⋅(0.92)2⇒⇒y=4.14 m

Cuestión c)

Sabiendo que el balón llegó a la portería en 1.61 s, su velocidad se obtiene:

vx=26.36⋅cos(20)=24.77 ms/vy= 26.36⋅sin(20)− 9.8⋅1.61=  −6.76 ms/v=vx2+vy2

√=(24.77)2+(−6.76)2−  √=25.67 ms/

Ejercicios para resolver👇:

Se patea un balón de fútbol con un ángulo de 37° con una velocidad de 20 m/s. Calcule:

a) La altura máxima.

b) El tiempo que permanece en el aire.

c) La distancia a la que llega al suelo.

d) La velocidad en X y Y del proyectil después de 1 seg de haber sido disparado

Imagenes 👍:

Videos 😎:

Links👴:
http://movimientoparabolicokrisia.blogspot.com/

http://blog.espol.edu.ec/fgmunoz/files/2011/06/parabolico-ejercicios1.pdf
http://genesis.uag.mx/edmedia/material/fisica/movimiento8.htm